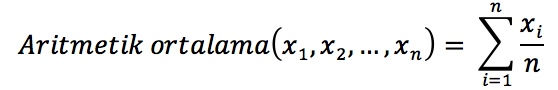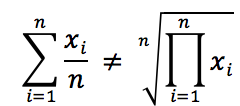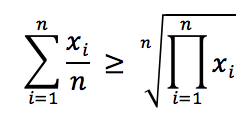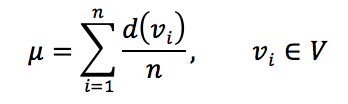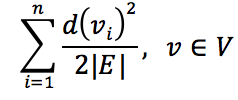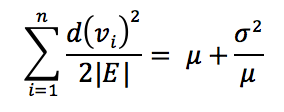Yazan : Şadi Evren ŞEKER

İstatistiksel olarak bir kişinin arkadaşlarının ortalama arkadaş sayısının o kişiden daha fazla olması durumudur.

Örneğin bir sosyal ağdaki x kişisinin arkadaş sayısı n ise, x kişisinin n arkadaşının ortalama arkadaş sayıları n’den büyüktür şeklinde tanımlanabilir.

Bu durumun sebebi basitçe bir kişinin sosyal ağdaki arkadaşlarının aslında sosyal ağdaki arkadaş sayısı çok olan kişilerden olması, sosyal ağda ortalamadan az arkadaşı olan kişilerin ise bu kişinin arkadaşı olması ihtimalinin zayıf olmasından kaynaklandığı söylenebilir.

Paradokssal kısmı ise çoğu kişini bu gerçeğin aksine, arkadaşlarının arkadaş sayılarından daha fazla arkadaşı olduğuna inanıyor olmasıdır [2].

Paradox ilk olarak Scott L. Fled tarafından 1991 yılında American Journal of Sociology’de yayınlanan makalesinde ele alınmıştır [1]. Günümüzde ise çoğu sosyal ağ ilişkisinin ve metriklerinin çıkarılmasında kullanıldığı söylenebilir.

Matematiksel Açıklama

Kavramın isminde paradoks geçmesine ve çoğu kişinin algısına göre bir paradoks olmasına karşılık vaka gerçekten istatistiksel olarak ispatlanabilir.

Öncelkle Aritmetik ve Geometrik ortalamaların eşitsizliği (literatürde AM-GM olarak arithmetic mean, geometric mean kavramlarının kısaltması olarak da geçmektedir) kavramının anlaşılması gerekmektedir.

Basitçe bir serideki değerlerin aritmetik ortalaması (arithmetic mean) ve geometrik ortalaması (geometric mean) birbirinden farklıdır. Bu ortalamaların formüllerini hatırlayacak olursak, aritmetik ortalama aşağıdaki şekilde yazılabilir:

Geometrik ortalama ise üstel olarak çalışmakta olup aşağıdaki şekilde yazılabilir:

işte aritmetik ve geometrik ortalamaların eşitsizliği aslında bu iki değerin birbirine eşit olmadığını söylemektedir yani aşağıdaki durum bir eşitsizliktir:

Daha kolay anlaşılabilmesi için durumu iki sayı için açıklayalım. Elimizde a ve b gibi iki tam sayı olsun. Bu sayıların aritmetik ortalaması toplamlarının yarısıdır ve geometrik ortalaması da çarpımlarının kareköküdür ve bu iki değer birbirine eşit değildir şeklinde modellenebilir.

Kavramı biraz daha ilerletecek olursak aritmetik ortalamanın geometrik ortalamadan her zaman daha yüksek olduğunu da söyleyebiliriz. Yani yukarıdaki modelimizi aşağıdaki eşitsizlik haline dönüştürmemiz doğru olacaktır:

Yukarıdaki büyük eşittir ifadesinin tek eşitlik durumu x=y için gerçek olmaktadır. Diğer bütün durumlarda büyüktür olarak düşünmek gerekir.

Sosyal Yapıya Uyarlanması

Öncelikle yukarıdaki eşitsizlik durumlarının bir sosyal ağa nasıl uygulanabileceğini anlatmaya çalışalım. Herhangi bir sosyal ağı, aslında yönsüz bir şekil (graph) olarak görmek mümkündür çünkü ağda bulunan her arkadaşlık aslında ağdaki her düğüm (kişi) arasındaki bir kenara (edge) karşılık gelmektedir ve A ile B arkadaş ise aynı zamanda B ile A da arkadaştır denilebilir. Bu durumda elimizde klasik olarak G = (V,E) şeklinde gösterilebilecek bir şekil (graph) bulunmaktadır.

Paradoksumuza geri dönecek olursak ortalama arkadaş sayısı aslında bu şekil üzerindeki her düğümün ortalama kenar sayısı olarak düşünülebilir. Graf teorisinde bir düğümün kenar sayısı o düğümün derecesi ( d(v) ) olarak ifade edilebilir. Bu durumda ortalama arkadaş sayısı aşağıdaki şekilde hesaplanacaktır:

Yukarıdaki denklemde n, düğüm sayısı ve d(v) herhangi bir düğümün derecesi olarak kullanılmıştır. Arkadaşlık ilişkisi, ikili bir ilişki olduğu için düğüm dereceleri kenar sayısının iki misli olacaktır. Yani aslında her düğümün bir komşusu için bu düğüm de başka bir düğümün komşusu olacaktır. Bu durumda yukarıdaki denklem aşağıdaki şekilde yeniden yazılabilir:

Yani kenar sayısının iki mislinin düğüm sayısına oranı olarak düşünülebilir.

Herhangi bir arkadaşın bir arkadaşının arkadaşları ise aslında ikili ilişkinin (arkadaşlık ilişkisi olan her bir kenar) üzerinden seçilmiş olan kenarların derecesi kadardır. Bu durum istatistiksel olarak iki olasılığın çarpılmasını gerektirir ve aşağıdaki şekilde gösterilebilir:

Yani herhangi bir arkadaşlık ilişkisinde (mesela a ile b arasında olsun) a’nın arkadaşı olan b’nin d(b) kadar arkadaşı olduğunu biliyoruz. Ayrıca tanım itibariyle bu d(b) değerinin içerisinde a ile b arkadaşlığının da olduğunu biliyoruz. Ve yine tanım itibariyle b’nin d(b) kadar arkadaşı olduğunun d(b) kadar arkadaşının değerleri içerisinde olduğunu da biliyoruz. Dolayısıyla d(b)’nin karesini alıyoruz. Bunu daha iyi anlayabilmek için a,b ilişkisinin aslında 1, d(b), d(b)2, ... şeklinde giden bir etkisi olduğu da düşünülebilir. Bu denklem ayrıca aşağıdaki şekilde de yazılabilir:

Yani basitçe standart sapmanın karesinin ortalamaya bölümü ile elde edilen sapma miktarının ortalamaya eklenmesidir. Buradaki ortalama ve standart sapmanın karesinin (çift fonksiyon olmasından dolayı da ) pozitif değerler olacağı bilinmektedir (eksi sayıda komşu olamayacağına göre ortalama değer her zaman pozitif olacaktır)

Denklemin paydası ise ortalama değer olarak her kenar için iki düğüm olacağı gerçeğinden yola çıkarak kenar sayısının iki mislini hesaplayarak bulunmaktadır.

Şimdi iddiamızı yeniden yazacak olursak aşağıdaki eşitsizlik olarak düşünülebilir:

Kısaca yukarıdaki bütün sembollerin pozitif değerler ile ifade edildiğini kabul edersek eşitsizliğin doğru olduğu ve ancak standart sapmanın sıfır olduğu durumda eşitlik olduğunu (ki bu durumda da bütün ağdaki kişilerin arkadaş sayısının birbirine eşit olduğunu) söyleyebiliriz.

Kaynaklar

[1] Feld, Scott L. (1991), "Why your friends have more friends than you do", American Journal of Sociology 96 (6): 1464–1477, doi:10.1086/229693, JSTOR 2781907.

[2] Zuckerman, Ezra W.; Jost, John T. (2001), "What makes you think you’re so popular? Self evaluation maintenance and the subjective side of the "friendship paradox"", Social Psychology Quarterly 64 (3): 207–223, doi:10.2307/3090112.